数据结构#
线性表#
顺序表#
顺序表是线性表的一种实现方式,采用一段连续的存储空间来存放线性表的元素。其特点是:
- 支持随机访问,可以通过下标直接访问任意元素。
- 插入、删除、按值查找时间复杂度为T=O(n)。
表内元素逆置:遍历前半部分,与后半部分交换位置。T=O(n),S=O(1)。
删除值为e的元素:遍历,用k统计非e元素个数,遍历时将非e元素放到第k个位置。T=O(n),S=O(1)。
合并有序顺序表:对比两表表头元素,较小的元素放入新表,指针后移。重复此过程直到一个表为空,将另一个表剩余元素直接放入新表。T=O(n),S=O(n)。
等长升序表A、B,求合并后新表中位数:双指针法,分别指向A、B的中间位置。比较两个指针所指元素,相等直接返回,若A[i] < B[j],则舍弃A[i]之前B[j]之后,在反复比较中间元素,直到找到中位数。T=O(n),S=O(1)。
链表#
删除指定节点p:将p的下一个节点的值赋给p,然后删除p的下一个节点。T=O(1),S=O(1)。但无法删除尾节点。
删除值为e的节点:初始化pre=L,p=L->next。遍历链表,若p->data == e,则将pre->next指向p->next,删除p节点。否则同步后移pre=p,p=p->next。T=O(n),S=O(1)。
单链表逆置:P=L->next,L->next=NULL。用P遍历L,依次将元素重新头插回L:Q=P->next,P->next=L->next,L->next=P,P=Q。直到P为空。T=O(n),S=O(1)。
单链表找倒数第K个节点:双指针法,先让p1走K步,然后p2从头开始,p1和p2同时走,直到p1到达尾节点,此时p2所指即为倒数第K个节点。T=O(n),S=O(1)。
判断单链表是否有环:快慢指针法,p1每次走两步,p2每次走一步,若有环则两指针必相遇。T=O(n),S=O(1)。
循环单链表判空:L->next == L (注意L是头节点不是首节点)
循环双链表判空:L->next == L && L->prior == L
静态链表:数组存储的链式结构,每个元素包含数据域和指针域。指针域存储下一个元素的下标。静态链表的优点是节省存储空间,缺点是随机访问困难。
栈、队列#
栈#
一个数组+初始为-1的栈顶指针top,栈顶进栈顶出,栈顶元素为top所指元素。入栈top++,将新元素放入top位置;出栈时将top位置的元素删除,top—。
共享栈:数组Data的[0]和[maxSize-1]分别作为栈A和栈B的栈顶,两栈同时向中间生长,当A.top+1 == B.top时,栈满。入栈时先判断是否满,再将元素放入对应位置。
链栈:和单链表类似,栈顶指针指向头节点L,进栈=头插法。
队列#
一个数组+初始为0的队头指针front和队尾指针rear。队尾进队头出,入队时rear++,将新元素放入rear位置;出队时front++,返回front位置的元素。出队后之前的空位无法再用:“假溢出”
循环队列:利用取余运算将数组逻辑上视作环。入队时 rear=(rear + 1) % maxSize,将新元素放入rear位置;出队时 front = (front + 1) % maxSize,返回front位置的元素。
但此时front==rear既可能空也可能满,我们可以少用一单元,将队满条件改为 (rear + 1) % maxSize == front。
串的模式匹配#
主串S,模式串T,求S中满足T的子串的起始位置。
暴力算法#
i,j分别指向S和T的起始位置,逐个字符比较。若S[i] == T[j],则i++,j++;否则i=i-j+2(即原先位置+1),j=0。直到j==T.length时,匹配成功,返回i-j。
T=O(mn),其中m为S长度,n为T长度。
KMP算法#
利用到之前扫面的信息,使得i不用回溯到i-j+2
匹配值(PM):对T中每个key,分析串头到该key的子串,其最长的相同前后缀长度。PM[i]表示T[0:i]的最长相同前后缀长度。
当S[i] == T[j]时,i++,j++;否则j = PM[j-1](即回溯到最长相同前后缀的末尾)
TBC
改进的KMP算法 TBC#
树、二叉树#
二叉树#
A
/ \
B C
/ \ \
D E F
/
G非空二叉树的叶结点数 = 度为2结点数 + 1
先序遍历——NLR:A B D E G C F
void preorderRecursive(TreeNode* root) {
if (!root) return;
cout << root->val << " ";
preorderRecursive(root->right);
preorderRecursive(root->left);
}
void preorderIterative(TreeNode* root) {
if (!root) return;
stack<TreeNode*> st;
st.push(root);
TreeNode* curr = root;
while (curr || !st.empty()) {
while (curr) {
cout << curr->val << " ";
st.push(curr);
curr = curr->left;
}curr = st.top(); //先把所有左节点push进栈,并开始处理最左节点
st.pop();
curr = curr->right;
}
}中序遍历——LNR:D B G E A C F
void inorderRecursive(TreeNode* root) {
if (!root) return;
inorderRecursive(root->left);
cout << root->val << " ";
inorderRecursive(root->right);
}
void inorderIterative(TreeNode* root) {
if (!root) return;
stack<TreeNode*> st;
TreeNode* curr = root;
while (curr || !st.empty()) {
while (curr) {
st.push(curr);
curr = curr->left;
}curr = st.top();
st.pop();
cout << curr->val << " ";
curr = curr->right;
}
}后序遍历——LRN:D G E B F C A
void postorderRecursive(TreeNode* root) {
if (!root) return;
postorderRecursive(root->left);
postorderRecursive(root->right);
cout << root->val << " ";
}
void postorderIterative(TreeNode* root) {
if (!root) return;
stack<TreeNode*> st;
TreeNode* curr = root;
TreeNode* lastVisited = nullptr;
while (curr || !st.empty()) {
while (curr) {
st.push(curr);
curr = curr->left;
}curr = st.top();
if (!curr->right || curr->right == lastVisited) { //如果当前节点无右子树,或右子树已经处理完
cout << curr->val << " "; //就可以处理当前节点
st.pop();
lastVisited = curr;
curr = nullptr; //同时将curr置空,等待处理下一个栈顶节点
} else {
curr = curr->right; //如果当前节点有右子树,要先处理右子树
}
}
}层次遍历:A B C D E F G
void levelOrder(TreeNode* root) {
if (!root) return;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* curr = q.front(); q.pop();
cout << curr->val << " ";
if (curr->left) q.push(curr->left);
if (curr->right) q.push(curr->right);
}
}先序、后序、层次任一遍历 + 中序可以唯一确定一课二叉树。因为前三者可确定根节点,中序可区分左右子树
先序 + 后序无法确定树,但可以确定结点间的祖先关系:如果先序xy,后序yx,则x一定是y祖先
森林#
双亲表示法:类似静链表,每项附设一个游标。每个结点存储其双亲结点的下标,根结点的双亲下标为-1
| 下标: | 0 (根) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 数据: | A | B | C | D | E | F | G |
| 双亲: | -1 | 0 | 0 | 1 | 1 | 2 | 4 |
孩子表示法:单链表数组,数组存所有节点,同时每个节点将他的孩子节点的数组下标用单链表连接起来
| 0:A | 1:B | 2:C | 3:D | 4:E | 5:F | 6:G |
|---|---|---|---|---|---|---|
| →1 | →3 | →5 | →6 | |||
| →2 | →4 |
二叉树表示法(孩子兄弟表示法):二叉链表,左指针指向第一个孩子节点,右指针指向第一个兄弟节点
利用二叉树表示法,可以将树和二叉树相互转化。将森林转为二叉树时,将不同树的根节点当作兄弟
相关应用#
并查集:
- 使用双亲表示法,每个结点存储其双亲结点的下标。
- 若两个结点的双亲相同,则它们属于同一集合。
- 查找时不断向上查找双亲,直到找到游标=-1的根结点。
- 合并时将一个集合的根结点的双亲指向另一个集合的根结点。
哈夫曼树:
- n个带权节点生成的二叉树,保证其带权路径长度最小。主要用于数据压缩。
- 每个叶子结点存储一个权值,非叶子结点存储两个子树的权值之和。
- 生成哈夫曼树时,每次选择权值最小的两个节点合并成新节点,新节点的权值为两个节点权值之和。
二叉排序树(BST):
- 二叉树的一种特殊形式,左子树节点权值 < 根节点 < 右子树的所有节点权值。使得中序遍历有序
- 插入时,若新节点小于当前节点,则递归插入左子树;否则递归插入右子树。
- 无法存在两个相等的节点
- 插入成功时节点一定在叶子节点,否则会破坏原有结构
平衡二叉树(AVL):
- 任意节点的左子树和右子树的高度差不超过1。
- 通过旋转操作保持平衡,分为左旋、右旋、左右旋、右左旋四种情况。
红黑树(RB-Tree):
- 一种平衡二叉排序树
- 根和叶子节点均为黑色(叶子节点一般虚拟)
- 父子不能同为红色
- 任意节点到其可到达的叶子之间都包含相同数量的黑节点
- n个节点的红黑树高度不超过2log(n+1),因此查找、插入、删除操作时间复杂度均为O(log n)。
- 查找效率比严格的平衡二叉树稍低,但增删时不用旋转
图#
存储#
邻接矩阵:n个顶点,使用n*n的二维数组存储,有边为1,无边为0
邻接表:单链表组成的数组,每个单链表表示该节点邻接的所有节点
遍历#
vector<vector<int>> adjList;
void BFS(int start) {
vector<bool> visited(V, false); // 访问标记
queue<int> q;
q.push(start);
while (!q.empty()) {
int v = q.front();
q.pop();
visited[v] = true;
cout << v << " "; // 访问该节点
// 访问所有未访问的邻接节点
for (int neighbor : adjList[v]) {
if (!visited[neighbor]) {
visited[neighbor] = true;
q.push(neighbor);
}
}
}
}
void DFS(int start) {
vector<bool> visited(V, false); // 访问标记
stack<int> s;
s.push(start);
while (!s.empty()) {
int v = s.top();
s.pop();
if (!visited[v]) {
visited[v] = true;
cout << v << " "; // 访问该节点
// 将未访问的邻接节点加入栈中
for (int neighbor : adjList[v]) {
if (!visited[neighbor]) {
s.push(neighbor);
}
}
}
}
}最小生成树#
是指在一个连通无向带权图中,找到一棵包含所有顶点的树,使得所有边的权值之和最小
Prim 算法(适合稠密图):任取一顶点加入集合,每次取距离该集合最近的点加入,T=O(|V|^2)
Kruskal 算法(适合稀疏图):将边长排序,从小到大选择,要保证不会形成环,T=O(|E|log|E|)
最短路径#
求图中某点到其他点的最短路径
Dijkstra算法:
简而言之,先将起点加入集合,之后每轮将加入集合的点纳入考虑并刷新路径之,再选择集合外路径最短的点加入集合,T=O(|V|^2)
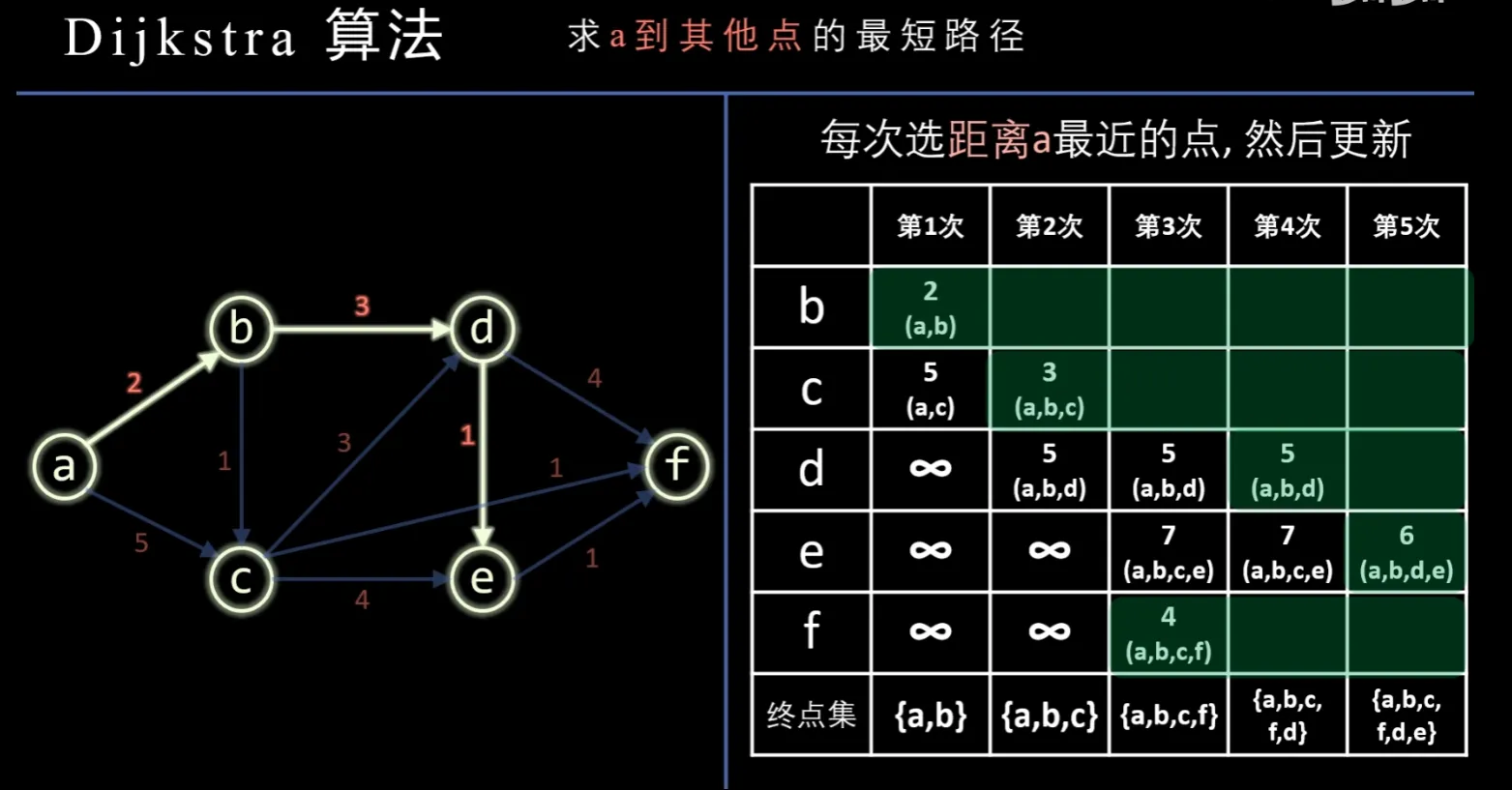
Floyd算法
拓扑排序#
以顶点表示活动的有向图(AOV网)中,每次输入一个无前驱的节点并删除它的相关边,最后生成的序列(不一定唯一)
关键路径#
以边表示活动的有向图(AOE网)中,从源点到汇点的最长路径。路径中的边成为关键活动。
寻找关键活动:分别计算活动最早和最晚开始的时间,若时间之差<=0则该边为关键活动
缩短关键活动不一定能缩短整个工程工期,但可能会使其变为非关键
查找#
二分查找#
int binarySearch(const vector<int>& arr, int target) {
int left = 0;
int right = arr.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2; // 防止溢出
if (arr[mid] == target) {
return mid; // 找到目标,返回索引
}
else if (arr[mid] < target) {
left = mid + 1; // 目标在右半部分
}
else {
right = mid - 1; // 目标在左半部分
}
}
return -1; // 未找到目标值
}B树#
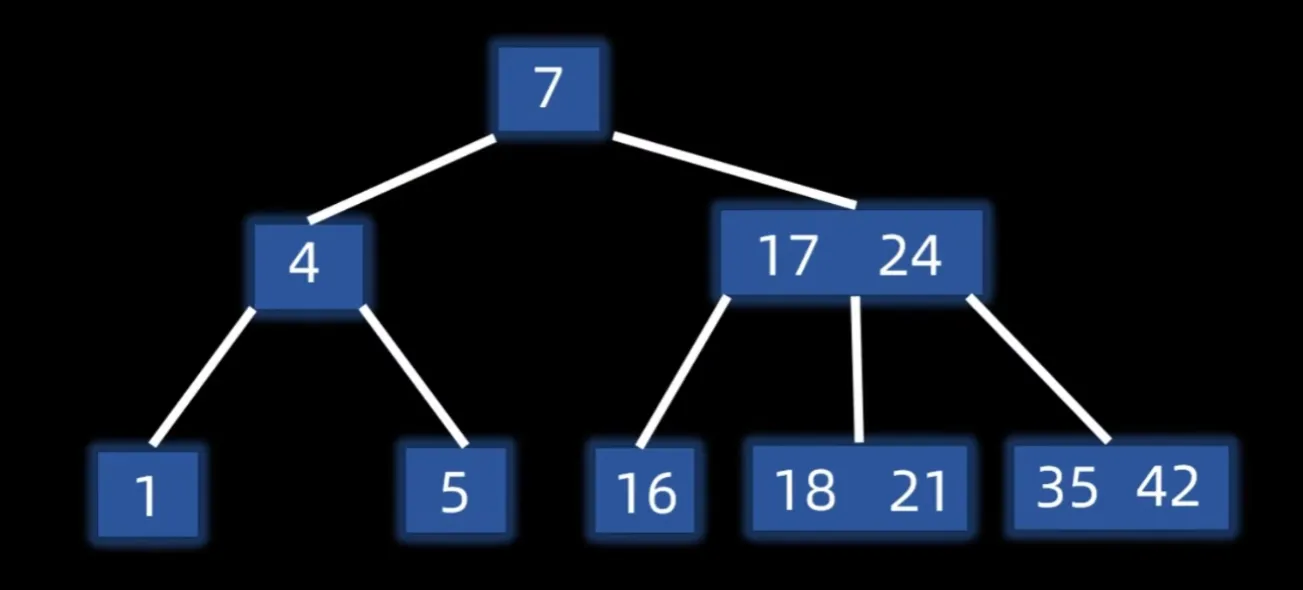
多路平衡查找树,对于一个m阶B树,每个节点最多m-1个key,m个子树
根节点最少2个子树,其他分支节点最少⌈m/2⌉个子树
所有叶子节点都在同一层且不带信息,视为查找失败
B+树#
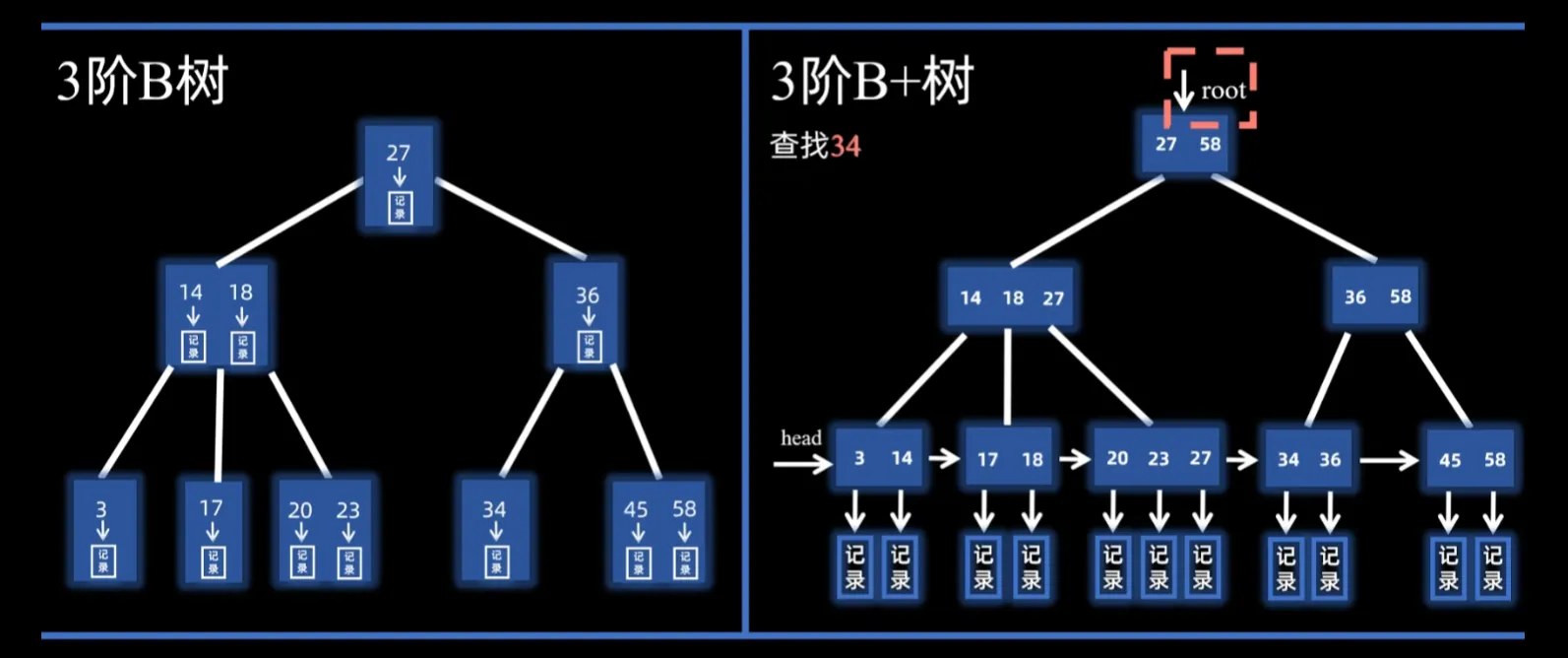
B树的数据存在分支节点,查找到叶结点时视作失败。但B+树的数据存在叶子节点,分支节点只做索引(表示对应子树中的最大key)
对于一个m阶B树,每个节点最多m个key,m个子树
根节点最少2个子树,其他分支节点最少⌈m/2⌉个子树
叶节点包含全部key,同时按顺序排列,相邻的叶节点之间相互连接
哈希表#
哈希函数构造方法
- 直接定址:H = a*key+b
- 除数:H = key mod p
- SHA
处理冲突
- 开放定址:地址既对同义项开放,也对非同义项开放,这样当发生冲突书可以使用线性探测、平方探测等再次选址
- 拉链法:所有同义项按链表方式存在同一空闲地址
哈希表的查找效率取决于散列函数、冲突办法和装填因子(记录/表长)。
排序#
| 排序算法 | 原理 | 时间复杂度 | 空间复杂度 | 稳定性 | 适合场景 |
|---|---|---|---|---|---|
| 插入排序 | 从头建立一个有序序列,每轮将后面的元素加入到前面的有序序列中 | 最坏/平均: O(n²), 最好: O(n) | O(1) | 稳定 | 小规模数据集,数据部分有序时效果好 |
| 希尔排序 | 基于插入排序的改进,将数据分组进行排序,再逐步减少分组间隔 | 最坏: O(n²), 最好: O(n log n) | O(1) | 不稳定 | 适用于中小规模数据,能提高插入排序效率 |
| 选择排序 | 每次选择最小(或最大)元素,与未排序部分的第一个元素交换 | O(n²) | O(1) | 不稳定 | 小规模数据集,或对内存使用敏感的场景 |
| 冒泡排序 | 重复比较相邻元素,并交换它们的位置,将最大的元素“冒泡”到末尾 | 最坏/平均: O(n²), 最好: O(n) | O(1) | 稳定 | 小规模数据集,或对效率要求不高的场景 |
| 快速排序 | 分治法:选取一个基准元素,将小于基准的元素放左边,较大的放右边 | 最坏: O(n²), 最好/平均: O(n log n) | O(log n) | 不稳定 | 大规模数据集,平均性能优秀,内存消耗小 |
| 堆排序 | 将数据构建成堆结构(通常是最大堆),然后反复取出最大元素并调整堆 | O(n log n) | O(1) | 不稳定 | 适用于需要优先队列的场景,如调度算法 |
| 归并排序 | 分治法:递归地将数组分割成两半,再合并两个已排序的子数组 | O(n log n) | O(n) | 稳定 | 大规模数据集,特别是外部排序 |
| 基数排序 | 按位数进行排序,逐位比较,通常与计数排序结合使用 | O(nk), k为位数 | O(n + k) | 稳定 | 数据范围较小且均匀分布的整数或字符串 |
| 桶排序 | 将数据分到有限数量的桶中,再对每个桶中的数据进行排序 | 最坏: O(n²), 最好: O(n + k) | O(n + k) | 稳定 | 数据范围已知且分布均匀的场景,如浮点数 |
void insertionSort(vector<int> &nums) {
// 外循环:已排序区间[0, i-1],待排序nums[i]
for (int i = 1; i < nums.size(); i++) {
int curr = nums[i],
int j = i - 1;
// 内循环:将 curr 插入到已排序区间 [0, i-1] 中的正确位置
while (j >= 0 && nums[j] > curr) {
nums[j + 1] = nums[j]; // 将 nums[j] 向右移动一位
j--;
}
nums[j + 1] = curr; // 将 curr 赋值到正确位置
}
}
void selectionSort(vector<int> &nums) {
int n = nums.size();
// 外循环:已排序区间[0,i-1],待排序nums[i]
for (int i = 0; i < n; i++) {
// 内循环:找到未排序区间内的最小元素
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (nums[j] < nums[minIndex])
minIndex = j; // 记录最小元素的索引
}
// 将该最小元素与未排序区间的首个元素交换
swap(nums[i], nums[minIndex]);
}
}
void bubbleSort(vector<int> &nums) {
int n = nums.size();
// 外循环:未排序区间[i,n-1],每次从右往左冒泡以修复nums[i]
for (int i = 0; i < n; i++) {
// 内循环:将未排序区间 [i, n-1] 中的最小元素交换至该区间的最左端
for (int j = n - 1; j > i; j--) {
if (nums[j] < nums[j - 1]) {
// 交换 nums[j] 与 nums[j - 1]
swap(nums[j], nums[j - 1]);
}
}
}
}
计算机组成原理#
系统概述#
冯诺依曼架构:
- 硬件系统:运算器 + 控制器 + 存储器 + 输入设备 + 输出设备
- 指令和数据同等地位存储在存储器中,按地址寻访,均为二进制
- 指令由操作码和地址码组成
- 指令在存储器中顺序存放,机器在指令驱动下自动执行
系统多级层次:
- 硬联逻辑级,由门电路、触发器等逻辑电路构成
- 微程序级,由微指令编写微程序,控制信息传送
- 机器语言级:用微程序解释机器指令系统
- 操作系统层
- 汇编语言层
- 高级语言层
- 应用语言层
数据的表示和运算#
存储器结构层次#
分类#
按作用分类
- cache:与CPU速度匹配,通常在CPU内
- 主存:内存,CPU可直接随机访问,并且可与cache、辅存交换信息
- 辅存:外存,不可与CPU直接交换数据
cache和内存间的交换由硬件自动完成,内存和外存间的交换由硬件和操作系统实现
按存取方式分类:
- 随机存储:RAM,存取时间与物理地址无关
- 只读存储:ROM,狭义上的只能随机读不能写,现在代表可以随机存取,但写入会慢几个数量级,且断电保留
- 串行访问:如CD等,不可随机存取,要按照物理地址的先后寻址
高速缓冲存储器 Cache#
局部性原理:
- 时间局部性:最近的未来要用的信息,很可能是现在正使用的信息
- 空间局部性:最近的未来要用的信息,很可能与现在正使用的信息物理上相邻
一致性和包容性原则:
- 一致性:多级存储体系中,同一信息可能同时存放在几个存储层次中,信息在这些层次中必须相同
- 包容性:内层信息一定被包含在各级外层存储器中
基于以上原理,cache将内存中频繁使用的数据复制,每次要使用时,若能直接在cache中找到,则可以极大提高效率。对于未找到的,在内存中访问完后立即调入cache
cache和内存的映射方式:
- 直接映射:根据内存块的地址以及cache块号,每个内存块装入cache的块号是唯一确定的,若该cache块已经存了其他内存块,则直接替换
- 全相联映射:每一个内存块可以装入任意一个cache块,CPU访存时需要检查cache中所有块以确定是否命中
- 组相联映射:将cache空间分组,组间使用直接映射,组内全相联,相当于上述两个方法的折中
cache替换算法:(直接映射直接替换,算法主要针对全相联和组相联)
- RAND:随即替换
- FIFO:选择最早调入的cache块进行替换
- LRU:近期最长时间未使用的块进行替换
- LFU:最不经常使用的块进行替换(不如LRU)
cache写策略:CPU对cache命中后,需修改命中的这块内容,如何保证这块内容在cache和内外存中的一致性
- 全写法:同时写入cache和内存对应块
- 写回法:只修改cache,当该cache块要被替换时再写回内存
虚拟存储器#
为了弥补内存空间的不足,将外存在逻辑上当作内存的地址空间,以虚地址形式访问。由辅助的软硬件将虚地址转换为外存的实际物理地址。
段式虚存#
将程序的存储按功能划分为相对独立的段,以段为单位进行内外存之间的调度。
使用段表指明每个段的段号、装入位(是否装入内存)、段起点、段长、访问方式等信息
分段一般与程序的自然分界对应,具有逻辑独立性,便于编译、共享。
但不固定的段长也不便内存分配空间,会造成内存碎片。
页式存储#
以固定长度的页面为基本单位,将内存和虚存都划分成固定大小的页。
虚拟地址可分为虚页号 + 页内地址两个字段,由页表实现从虚地址到实地址的转换
页表位于内存中,存放虚页号与实页号的映射,指明装入位、脏位(写回机制)、引用位、物理地址等。
CPU的指令中是虚拟地址。执行指令时:
- 根据每个进程的页表基址寄存器找到该进程的页表首地址
- 根据虚拟地址的高位(也就是虚页号)在页表中找到对应的页表项
- 若该页表项的装入位为1,代表该页已经装入内存。此时根据页表项对应的实页号,再加上虚拟地址的低位(页内地址)找到实际的物理地址
- 若该页表项装入位为0,代表该页还未装入内存,需要操作系统进行缺页处理
在上述机制中,每次访存都需要查一次页表,增加了访问主存的次数。系统引入了基于局部性原理的快表机制(TLB),类似cache,将满足局部性的页存在TLB中,提高访存效率
指令系统#
指令格式#
一组二进制代码,分为操作码字段和地址码字段
- 零地址指令:只有操作码OP,没有显式地址,如空操作、停机、关中断指令等
- 一地址指令:操作码OP + 地址码A1,按A1地址取出数据进行OP操作后再放回原地址,如+1、-1、求反等
- 多地址指令:OP + A1 + A2 +。。。
寻址方式#
指令寻址:找下一条将执行的指令的地址#
一般由程序计数器PC给出。
顺序寻址时,每执行一次指令PC自动+1(指一条指令占的地址长度,如指令长2B,则按字节编址就是+2)
对于变长指令,CPU会先读一个字节,根据OP码判断指令长度并据此修改PC值
需要转移类指令时,会根据当前操作数(跳转)修改PC值
数据寻址:确定本指令地址码的真实地址#
数据寻址方式较多,通常在指令中设一字段指明采用哪种寻址方式,如 OP + 寻址特征 + 形式地址A1 + 寻址特征 + 形式地址A2 。。。
- 直接寻址:形式地址A就是逻辑地址EA,即EA = A
- 间接寻址:A指向的单元中存放了EA的地址,即 EA = (A),类似指针,可以多次间址
- 寄存器寻址:A是寄存器的地址EA = R
- 寄存器间接寻址:A是寄存器地址,但存储的是逻辑地址,EA = (R)
- 立即数寻址:A就是操作数本身,一般是补码形式
- 基址寻址:基址寄存器BR中的内容 + A 才是逻辑地址,EA = (BR) + A,一般来说 (BR) 不可变
- 变址寻址:变址寄存器IX的内容 + A,即 EA = (IX) + A,一般来说 (IX) 作为偏移量可变,而A不变
- 相对寻址:A是下一条指令位置的偏移量,即 EA = (PC) + A,一般用于跳转指令
- 隐含寻址:一些特殊指令如ADD,隐含的规定的ACC寄存器作为第二操作数地址
指令集#
CISC:复杂指令集,包含指令条目多,功能覆盖广,指令长度可变,寻址方式多样,一般采用微程序实现,如x86架构
RISC:根据使用频率,只选择最经常用的简单指令,其他功能依靠指令间的组合实现。指令长度固定、格式单一,如arm架构
中央处理器#
功能和结构#
功能:指令控制、操作控制、时间控制、数据加工、中断处理
基本结构:
- 运算器:数据加工的中心,由算术逻辑单元ALU、暂存寄存器、累加器ACC、通用寄存器组、状态寄存器PSW、移位器、计数器CT组成
- 控制器:
- PC:程序计数器,存放下一条指令的内存地址,有自增功能
- IR:指令寄存器,保存当前执行的指令
- ID:指令译码器,将指令的OP字段送至ID,提供特定的操作信号
- MAR:内存地址寄存器,存放指令需要访问的内存地址
- MDR:内存数据寄存器,存放向主存读或者写的信息
- 时序系统:产生时序信号
- 微操作信号发生器:根据(IR)、(PSW)以及时序信号,产生控制信号
指令执行过程#
指令周期:CPU取出并执行完毕一条指令的时间,通常由若干机器周期组成,如 取指令 + 取有效地址 + 执行指令 + 等待中断。这些指令周期又包含若干时钟周期
一个完整的指令周期一般包括:取指周期 + 间指周期 + 执行周期 + 中断周期
为了区别不同周期,CPU内置4个标志触发器,FE、IND、EX、INT,分别对应上述四个周期
取指周期:根据PC的内容从内存中取出指令并放入IR#
- 将PC的内容保存至MAR,MAR在将地址通过地址总线传给内存:(PC) -> MAR -> 地址总线 -> 内存
- CU通过控制总线将读信号发给内存: CU:(1->R) -> 控制总线 -> 内存
- 内存通过数据总线,将相应地址的内容传给MDR,再交给IR: 内存 -> 数据总线 -> MDR -> IR
- CU发出控制信号,使PC+‘1’:(PC) + 1
间指周期:取得操作数的有效地址#
- 将指令中的地址码送给MAR,再经MAR转发给内存:Ad(IR) 或 Ad(MDR) -> MAR -> 地址总线 -> 内存
- CU发出读信号给内存:CU:(1->R) -> 控制总线 -> 内存
- 内存通过数据总线,将有效地址存到MDR:内存 -> 数据总线 -> MDR
执行周期:取操作数,根据IR中的指令操作码,通过ALU产生执行结果#
中断周期:暂停当前任务,保存断点并处理中断,一般使用堆栈#
假设使用SP指示栈顶地址,由于计算机中的堆栈是向低地址增加,所以进栈操作是SP-1
- CU控制SP-1,并传给MAR,再通过地址总线传给内存: SP-1,(SP) -> MAR -> 地址总线 -> 内存
- CU发出写命令,并通过控制总线传给内存: CU:(1->W) -> 控制总线 -> 内存
- 将PC中的信息写进内存的地址为SP的单元中: (PC) -> MDR -> 数据总线 -> 内存
- CU将中断服务的入口地址传给PC:CU -> PC
指令流水#
总线#
IO#
操作系统#
系统概述#
CPU运行级别#
内核程序:管理者,可执行除trap之外的所有指令,常见特权指令如IO、中断。内核程序在核心态执行 应用程序:用户自编程序,此时CPU处于用户态,无法执行特权指令
内核态 -> 用户态:执行中断返回指令,该指令修改PSW,修改CPU状态 用户态 -> 内核态:通过中断信号,OS进入内核态,停止当前应用程序,转而执行中断处理程序
中断和异常#
异常(内中断):来自CPU内部,与当前指令有关
- 陷入:Trap,应用程序在请求内核服务时,会加入一条Trap指令,进而引发中断处理,将控制权转给内核以进行内核服务
- 故障:Fault,一些错误条件导致(如缺页故障),内核修复故障后会交换用户程序继续执行
- 终止:Abort,一些致命错误(如除0,非法使用特权指令),内核会直接终止当前程序
中断(外中断):来自CPU外部设备,CPU在每个CLK的末尾进行检查
- 时钟中断:任务的时间片已到,由时钟部件发出,CPU交由处理时钟中断的内核程序处理
- I/O中断:外部设备发出的信号,CPU同理交由相应内核程序处理
外中断处理流程:
- 关中断:硬件级别。CPU响应中断后,保护现场,不再响应其他更高级中断
- 保存断点:硬件级别。保存原先程序的(PC)
- 中断服务程序寻址:硬件级别。查询中断向量表(由OS初始化),确定相应的中断服务程序,将其入口地址传给PC
- 保存现场和屏蔽字:软件级别。保存PSW和某些通用REG的内容
- 开中断:硬件级别。此时允许响应更高级的中断
- 执行中断服务程序
- 关中断:硬件级别。准备恢复现场,恢复的过程也不能相应其他中断。
- 恢复现场和屏蔽字。
- 开中断,中断返回
系统调用#
广义上的指令,是OS提供给应用程序使用的接口,应用程序可以执行Trap发起系统调用,请求OS内核服务,OS转为核心态提供相应处理后在返回用户态
凡是与共享资源有关的操作,都需要应用程序访管,交由OS处理,如设备管理、文件管理、进程控制、进程通信、内存管理等
进程管理#
基本#
进程是程序的一次执行过程,是OS进行资源分配和调度的独立单位,动态
进程映像 = PCB + 可共享程序段 + 数据段 ,反应进程某个时刻的状态,静态
进程控制块PCB
- PID:独一无二的进程ID,属于用户ID下
- 进程控制和管理信息:包括CPU、磁盘等资源使用情况,进程当前状态等
- 资源分配清单:显示正在使用的文件、内存区、IO设备等
- 处理机相关信息:PSW、PC等Reg值,用于进程切换
进程状态:
- 创建态:OS为新进程分配PID,并申请PCB,然后为进程分配资源(分配成功则就绪,资源不足则阻塞)
- 就绪态:进程获得除CPU外的一切所需资源,处于就绪队列,等待上CPU
- 阻塞态:进程因等待某事件而暂停,如等待非CPU资源,IO完成等,此时及时CPU空闲也无法运行,位于阻塞队列
- 运行态:正在CPU上运行的进程
- 挂起态:位于就绪态或阻塞态是,进程可能暂时被调到外存等待
进程状态转换: 创建态 —> 就绪态 <—> 运行态 —> 终止态
- 就绪 -> 运行:进程被OS调度上CPU
- 运行 -> 就绪:时间片已到或CPU被抢占
- 运行 -> 阻塞:进程使用系统调用申请某资源或等待某事件
- 阻塞 -> 就绪:申请的资源被分配,或等待的事件已发生
进程通信IPC#
进程是资源分配的单元,各进程间的内存空间相互独立,无法直接访问其他进程的地址空间
- 共享存储:OS在内存中划分一块共享存储,通过互斥操作实现各进程对共享空间的RW。
- 消息传递:
- 直接通信:指明接收进程PID,通过发送原语直接传递信息,会挂到目标进程的消息队列上等待接收
- 间接通信:发送到某中间实体(信箱),接收方从信箱中接收
- 管道通信:Pipe,内存中一片固定的缓冲区,单Pipe半双工,双Pipe全双工。OS控制Pipe的互斥访问,管道写满时则写进程阻塞,读空时则读进程阻塞
线程#
线程是CPU的基本执行单元,程序执行流的最小单位,引入线程使得进程内部也可并发
进程是OS资源分配的基本单元,线程是CPU资源分配的基本单元。
每个线程有一线程ID和线程控制块TCB,几乎不拥有系统资源,只是在运行时共享所属进程的资源。
同进程的线程切换开销很小,由于共享地址空间,同进程的线程通信甚至无需OS干预
线程实现:
- 用户级线程:ULT,线程管理的所有工作由应用程序完成,内核意识不到现成的存在,进程内的线程切换在用户态下,同时一个线程阻塞,整个进程都阻塞,且多个线程无法上多核CPU并行。
- 内核级线程:KLT,真线程。线程管理由OS完成,程序只有到内核线程的编程接口,OS通过TCB管理线程。线程切换需要变态,一个KLT阻塞,其他KLT不受影响。
处理器调度#
调度层次:
- 作业调度:按照规则将合适作业调度内存,并为其创建相应进程。相当于 无 -> 创建态 -> 就绪态
- 内存调度:从进程的挂起队列中选择合适进程调回内存,相当于 挂起态 -> 就绪态
- 进程调度:从进程的就绪队列中选择合适进程上CPU,相当于 就绪态 -> 运行态
调度算法:
- FCFS:先来先服务。排队式,非抢占,不会导致饥饿。
- 对长作业有利,短作业不利
- SPF:短作业优先。每次调度选择队列中需CPU时间最短的进程上机。
- 非抢占,会导致饥饿。短作业有利
- SRTN:最短剩余时间优先。SPF的抢占式版本
- HRRN:高响应比优先。每次调度时计算各进程或作业的响应比((等待时间+所需时间)/所需时间)
- 非抢占,不会饥饿,对短作业有利
- RR:时间片轮转,抢占式,不会饥饿
- 优先级调度
- 多级反馈调度:设多个队列,优先级依次降低,时间片依次增大,上级队列空闲时才允许处理下级队列。
- 各队列FCFS,新进程加入最高级队列的队尾,若经过高级队列处理未处理完,则加入低级队列队尾。
- 被抢占的进程放回原队列队尾。
- 会导致饥饿(如果源源不断有进程加入,则低级队列得不到处理)
进程同步#
同步的主要任务:约束并发带来的异步性,让程序的执行具有可再现性
互斥准则:空闲让进、忙则等待、有限等待、让权等待(不能进临界区则放弃CPU)
互斥的软件实现:
- 单标志法:设置一个公用变量turn,指示允许进入临界区的进程ID。进程使用完后再修改turn让给其他进程。
- 谦让算法,违背了“空闲让进、让权等待”
- 双标志先检查法:设一布尔数组,标志各进程是否在用临界区。进程进入前先检查数组的其他值,若有true则等待,若全false则将自身flag标为true并进入,用完后改为false。
- 检查和上锁并非一气呵成,可能同时进入临界区,违背“忙则等待、让权等待”
- 双标志后检查法:先将自己的flag设为true,在检查其他flag。
- 同样,如果两个进程同时设true,则都进不了。违背“空闲让进、有限等待、让权等待”
- Peterson算法:既设置flag数组又设置turn标志。进程先将自身flag设为true,再将turn设为对方,并检查若对方flag=1且turn=对方则等待,否则进入临界区
- 用flag表意愿,用turn表谦让,但仍然违背 让权等待
互斥的硬件实现:
- 中断屏蔽:用开/关中断指令实现,但不适合多处理机,并且只能用于内核级进程(交给用户太危险)
- TSL指令:检查上锁状态,无论是否已上锁,再上锁,返回原来状态,即 while(TestAndSet(&lock)) ,若原先上锁,则空等;若未上锁,则上锁并进入
- Swap指令:略了,上述硬件实现也都不满足让权等待
信号量机制:信号量指OS中该类资源数量的变量,初始为数量,通过一对PV原语控制
- 整型信号量:消耗资源时用wait(等待信号量S。若S>0则-1,标志将使用一个资源),使用完毕后用signal(S++)
- 互斥的实现:设置互斥信号量mutex=1即可
- 同步的实现:设置同步信号量S=0;在需要后执行的代码前加入P(S),需要先执行的代码后加入V(S),这样只有V(S)执行后,P(S)才通过
经典同步问题:
- 生产者-消费者
- 一组生产者进程和一组消费者进程共享一初始为空,大小为n的缓冲区
- mutex=1用于互斥访问,full=0记录缓冲区使用的数量,empty=n记录空区数量
- 生产者:P(empty) -> P(mutex) -> 生产 -> V(mutex) -> V(full)
- 消费者:P(full) -> P(mutex) -> 消费 -> V(mutex) -> V(empty)
- 吸烟者:生产者生产多种产品 多消费者
- 生产者生产材料,对应的消费者消费并提示生产者继续生产
- Offer1=0、Offer2=0、Offer3=0 对应生产者产出材料;finish=0 标志消费者的完成信号
- 生产者:生产 -> V(相应Offer) -> P(finish)
- 消费者1:P(Offer1) -> 消费 -> V(finish)
- 读者-写者
- 一组读者和一组写者共享一个文件
- 互斥:rw=1标志写者的互斥访问;count=0记录正在读的数量;mutex=0保证对count的互斥
- 读优先:只要有读就无法写:
管程:一种高级同步机制,使得程序员不用再关注复杂的PV操作,而是将共享资源的操作封装,每次仅允许一个进程进入
死锁#
死锁的必要条件:
- 互斥:进程对互斥资源的争抢
- 不剥夺:进程所获资源在未使用完毕前,不得被其他资源抢夺
- 请求并保持:进程保持资源的情况下,又提出新的资源请求。由于该资源被占用不得不阻塞,但又对已有资源保持不放
- 循环等待:存在进程资源的循环等待链
- 死锁一定有循环等待,但循环等待不一定死锁(除非每类资源都只有一个)
死锁预防:
- 破坏互斥条件:将互斥资源资源改造成允许共享
- 破坏不剥夺条件:
- 进程请求资源无法满足时,立即释放现有资源
- 所需资源被占用时,由OS协助强行剥夺
- 破坏请求和保持条件:静态分配,运行前申请所需全部资源,未满足则不运行。但这会导致资源利用率低,导致饥饿
- 破环循环等待条件:顺序资源分配,给资源种类编号,规定进程只能按照顺序申请资源,且同类资源一次性申请完。会导致资源浪费
避免死锁:银行家算法
- 允许进程动态申请资源,但每次分配前计算分配安全性,安全则分配,不安全则等待
- 安全状态指OS的剩余资源可以按照某顺序一次满足进程的需求,从而使每个进程都可以完成
- 算法:n个进程,m种资源,设置各进程最大需求量Max矩阵(n*m)和已分配矩阵Alloc(n*m),以及Need = Max - Alloc
- 对于某进程的一次申请,判断是否在他需要的范围内 Request <= Need
- 接着判断系统是否可以满足申请
- 接着尝试分配并执行安全性算法,若都满足则分配,否则阻塞
死锁解除:
- 资源剥夺:挂起某些死锁进程,将其资源分配给其他资源
- 撤销进程:按优先级和代价强制撤销某些死锁进程
- 进程回退:让某些进程回退到足以避免思索地地步
内存管理#
程序装入步骤:
- 编译:由源代码生成目标模块
- 链接:由目标模块生成装入模块,链接以形成完整的逻辑地址
- 装入:将装入模块装入内存,有了物理地址
页式存储#
将内存分成大小相等的页框(页帧、物理页、块),从0开始编号,将进程页分为同样大小的分区,称为页。OS以页框为单位为各进程分配内存,每个页对应一个页框,不用连续存放。
OS会为每个进程建立一张页表(在进程的PCB中),其中每个页表项包含页号和页框号的对应关系(页号隐含)
确定物理地址:
- 通过逻辑地址得到该地址所在的页号以及页内偏移
- 查页表,通过页号得到页框号
- 通过页框号得到块地址,加上页内偏移得物理地址
地址转换机构:
- 页表寄存器PTR:OS使用PTR存放页表在内存中的起始地址F和表长M,当某进程被CPU调度时,就从它的PCB中得到F和M放入PTR。对于逻辑地址A,首先根据OS设置的页大小(假设为2^n bit)就可知A的后n位为页内偏移,前面的都是页号。
- 快表TLB:一种cache,集成在CPU内部,用于存放最近访问的页表项副本,通过时空局部性加快地址变换速度。TLB命中时,可以直接得到物理地址,节省了访问页表的一次访存开销。
- 多级页表:通常页表在内存中以连续块存放。但页表太大时,也可以将页表分组装入页框,为离散的页表再建一张页表。
虚拟内存#
根据局部性原理,作业无需一次性调入内存就可以运行,并且运行时也无需常驻内存,可以多次换进换出。因此可以在逻辑上扩充内存,使用户看到的容量远大于实际。逻辑地址对应的内容不一定可以直接在内存中找到,也许还需要从外存中调进来。
请求分页管理方式:在分页基础上,页表项中增添一些列
- 状态位:表示该页是否在内存中(如果不在,页表项中的物理页框号也没有意义)
- 访问字段:最近访问次数或上次访问时间等,共置换算法参考
- 修改位:该页调入内存后是否被修改过
- 外存地址
缺页中断: OS根据逻辑地址找到页表项后首先会检查状态位,若不在内存中则引发缺页中断。中断处理会将目标页调入内存并修改相应页表项。一个指令可能会产生多次缺页中断。
页面置换算法:
- 最佳置换:换出将在最长时间不再被使用的页。只是理论上,无法实现。
- 先进先出FIFO:会导致belady异常————有时候增加物理块反而会让缺页率不降反升(因为FIFO完全不考虑页面的访问频率或最近访问时间)
- 最近最久未使用LRU:经典手撕,双链表+hash
- 时钟置换NRU
驻留集:OS给一个进程分配的物理块的集合。驻留集太小会导致频繁缺页(抖动),太大会降低程序的并发度。
工作集:某时间窗口内进程实际访问物理块的集合。
文件管理#
文件本身结构:
- 无结构:又称流式文件,以字节为单位顺序组织成记录并积累。如txt、exe、png、mp4、c源代码。对记录的访问只能穷举搜索。
- 顺序文件:记录按照时间或关键字的顺序排列。如早期的工资单文件。
- 索引文件:建立一张索引表加快检索。如图书馆数目索引。
文件目录结构:
计算机网络#
概述#
网络性能指标
- 发送时延:传输时延,分度的第一个比特开始推送到最后一个比特推送完毕的时间,t = 数据长度 / 发送速率
- 传播时延:比特在信道中的传播时间,t = 信道长度 / 点播在信道中的速率
- 处理时延:节点为存储转发进行的必要处理时间(检错、找出口等)
- 排队时延:节点在路由I/O口排队的时间
- 时延带宽积:传播时延 * 信道带宽
- 往返时延RTT:从发送数据完毕到接受确认信息的时间(不包括发送时延),RTT = 2 * 传播时延 + 末端处理时间
网络分层模型:每层拥有各自的协议数据单元PDU,由服务数据SDU + 协议数据PCI组成。SDU就是上层的PDU,加入本层的PCI之后,交给下层。层层传递直到物理层
OSI7层参考模型:自上而下
- 应用层:用户使用的应用程序接口
- 表示层:两系统间数据格式转换、加密解密
- 会话层:建立、管理和终止会话
- 传输层:PDU——报文段(TCP)或数据报(UDP)
- 提供端到端的可靠传输,差错控制、流量控制等功能
- 协议:TCP、UDP
- 网络层:PDU——数据报
- 将数据报分组从源端点对点地传到目的端,为不同主机提供通信服务
- 协议:IP、ICMP、ARP、OSPF
- 数据链路层:PDU——帧
- 将网络层传来的IP数据报封装成帧,提供差错控制,流量控制、信道访问控制等
- 协议:SDLC、HDLC、PPP、STP
- 物理层:PDU——比特流
- 负责比特流的透明传输
- 协议:一般成为接口标准,如RJ45、IEEE802.3等,主要规定电路接口参数、传输信号意义、电气特征等
实际TCP/IP四层模型:
- 应用层:OSI上三层
- 传输层:TCP + UDP
- 网际层:IP
- 网络接口层:OSI下两层
物理层#
通信基础#
码元:固定时长的信号波,代表不同离散数值的基本波形
波特率:单位时间码元的传递个数
奈奎斯特定理:波特率存在上限,在理想低通,带宽为W(hz)时,波特率最大为2W,否则会出现码间串扰。
香农定理:在带宽受限且存在噪声干扰的信道中,比特率有上限
- 信噪比: S/N = 10lg(Ps/Pn),其中Ps为信号功率,Pn为噪声功率
- 最大比特率: C = W * log2(S/N)
编码#
物理层设备#
中继器:对数字信号做还原再生,回复线路中的损耗,以增强传输距离。仅作用于信号,不对数据包进行分析或处理。
集线器:多端口中继器,一个I口,多个O口,不具备定向能力,多个O口平分带宽(因为一个clk仍然只传一组数据)
数据链路层#
功能#
为网络层提供服务
- 无确认的无链接服务:丢失帧后DLL并不负责而是交由上层
- 有确认的无链接服务:无线通讯
- 有确认的面向连接服务
透明传输:将上层数据包封装成帧(添加首部和尾部)透明传输(无论什么样的比特组合,对DLL来说都是透明的),需要帧定界和同步功能
- 字符计数法:首部使用第一个字节标明帧内字节数
- 字符填充法:声明SOH(00000001)和EOT(00000100)标志帧的开始和结束
- 零比特填充法:用01111110标志开始和结束,在数据中插入额外的零比特,以避免特定比特模式的出现
差错控制(零比特差错) 当然,随着网络发展,目前已不再需要DLL提供差错控制功能
- 检错码
- 奇偶校验码
- 循环冗余码
- 纠错码
- 海明码
流量控制和可靠传输:DLL基于控制相邻节点间的应答,进行流量控制
- 停止等待协议:发送窗口和接收窗口均为1。发送方发送一帧后等待接收方的确认,收到确认后再发送下一帧,802.11
- 后退N帧协议:发送窗口 > 1,接收窗口 = 1。发送方可以在等待确认的同时发送多帧,但接收方只能按顺序接收,遇到有一帧超时,后面的帧全部重传
- 选择重传协议:发送窗口和接收窗口均 > 1。发送方可以在等待确认的同时发送多帧,接收方可以对收到的帧进行确认,未收到的帧可以选择性重传
介质访问控制MAC:对使用介质的每个节点隔离来自同一信道的其他信号
- 划分信道:包括频分复用、时分复用、码分复用等
- 随机访问划分:
- ALOHA协议:不做任何处理,若超时就认定信道中发生冲突,等待随机时间后再重传
- CSMA协议:载波侦听,发前检测信道是否空闲,忙则等待
- CSMA/CD:加入碰撞检测的载波侦听,在CSMA的基础上边发送边侦听。如果信号在总线的单程传播时延为τ,则至多2τ内就能确定信息是否碰撞(争用期)。节点必须在发送完之前得知是否发生碰撞,若发生则停止发送,等待随机时间后重传。因此每帧的发送时间 > 2τ,据此可求得最小帧长。
- CSMA/CA:加入碰撞避免的载波侦听。多适用于无线网络。
- 轮询访问:令牌环网
局域网#
广播信道、范围小、速率高、延迟低、可靠性强
以太网:总线型、CRC检测、CSMA/CD
- 以MAC帧作为以太网在DLL的PDU
802.11无线局域网:星型、CSMA/CA
广域网#
范围广、点对点、分组交换
PPP协议:不可靠,通过拨号或专线进行点对点传输
HDLC:可靠,面向比特的协议,提供帧的封装、差错检测和恢复等功能
DLL设备#
网桥:根据MAC帧地址对帧进行转发和过滤,可以隔离冲突域,提高吞吐量
交换机:自学习的多接口网桥,可以隔离冲突域,仍然无法隔离广播域